01：通信的基本概念

01 Chapter 1：通信的基本概念

1 基本概念

通信的需求起源于人们想要把一段信息传输到另外一个地方去。如果距离近，例如两人面对面，那只需要开口说话就行了，但一旦距离很远，通信需要各种各样的工程方法。

1.1 信息，消息与信号

例1：Alice想要传递“一起去旅游”的信息给Bob，她可以写短信，可以打电话，可以发起视频聊天，这代表着信息能够被表达成不同的消息。而她无论采取哪种方式，最终都会变成电磁波传播出去。也就是消息会被转换成信号。

Information(信息)：就如同例1中讲述的一样，无论采取短信，电话还是视频聊天，最终表达的意思是一样的，蕴含在这些形式中的东西称之为信息，它是我们要表示和传送的对象。
Message(消息)：对于同一个表达的意思，我们可以有很多种表达方式，可以说消息是信息的载体。
Signal(信号)：现代通信系统中一般指代电磁波，我们拿到了消息，需要将其转换为电磁波再通过天线发送出去。所以信号是消息的承载者。

1.2 模拟信号与数字信号

信号实际上是有两个维度的，第一个维度是时间，第二个维度是取值。我们可以简单排列组合这两个维度的连续与离散情况。例如时间连续取值离散，时间离散取值连续等等。

模拟信号：取值连续，时间连续或离散的信号
数字信号：取值离散，时间连续或离散的信号

可见，取值离散的我们才能称之为数字信号，这是因为数字电路或者计算机中无法存储精度无限的值。

1.3 通信与通信系统

例2：Alice准备发送消息了，她选择使用手机打电话。Alice的声音被转换为电磁波，通过天线在空气中传播到运营商的通信设备里，最终传输到了Bob的手机上。

通信：如例2中Alice用手机打电话一样，使用电信号来传输包含信息的消息就是通信。
通信系统：在例2中，Alice的语音是通过了一系列设备，包括手机，运营商设备，空气等等传到了Bob电话里，这一系列完成通信过程的电子设备和信道(在这里是空气)就是通信系统。

2 通信系统

2.1 系统框图

在例2中，我们看到了一整个通信过程。Alice生成了信息，她是信息源，手机以及手机中的天线发送了信号，它们是发送设备。空气作为了传输的信道，因为电磁波在空气中传播，而更多的传输过程发生在了运营商设备中。Bob的手机则是接收设备，Bob作为信息的接收者是信宿。

一般通信系统

graph LR
A[source]
B[Transmitter]
C[Transmission System]
D[Receiver]
E[Destination]
A-->B-->C-->D-->E

有些时候这个框图也比较常用

graph LR
A[信息源]
B[发送设备]
C[信道]
D[接收设备]
E[信宿]
F[噪声源]

A-->B-->C-->D-->E
F-->C

mermaid语法自动排版框图，所以上面这个图歪了，信息源，发送设备，信道，接收设备，信宿是一条直线，噪声源在信道下方指向信道。参考教材或Slides即可

Transmitter：将消息转换为适合信道传输的信号
Channel：信号传输的媒介
Receiver：将信号转换为消息
Recipient(信宿或受信者)：消息的目标物体。

2.2 系统指标

例3：Bob喜欢看网络视频，他不喜欢网络速度太慢，这样要等很久才能看得到接下来的画面。Bob也喜欢玩网络游戏，但他不希望网络游戏的信息传输出现错误。也就是说，我们希望通信系统既高效(efficiency)又可靠(Reliability)。

为了提升efficiency，我们发明了信源编码，它包括了AD转换，数据压缩等来减少信息中的冗余，尝试用更少的二进制数字来表示信息。因为要传输的东西通过编码变少了。所以efficiency提高了

为了提升reliability，我们发明了信道编码，它通过增加冗余来让信号在未知信道中也能可靠传输。典型代表就是纠错和检错能力。通过携带额外的信息让接收端有能力发现传输中的错误，甚至修改错误。

2.3 数字通信系统

数字通信系统使用二进制码来进行通信，虽然你还没有学，但它有以下性质

• 优点

  • 抗干扰能力强
  • 差错控制
  • 易于处理，传输，存储
  • 易于从不同信息源传输信号
  • 易于整合与加密

• 缺点

  • 需要更大传输带宽
  • 需要同步

2.4 通信系统不同的工作方式

例4：

• NASA向太空发送了一个旅行者号卫星，上面承载着人类文化的信息，但我们可能永远收不到回信。这是一种只有发送者向接收者发送的通信。
• 对讲机在其中一个人说话的时候，另一个人不能同时说话，而另一个人说话的时候，原来那个人就不能说话，这是一种双方同时只能有一个人作为发送者，另一个人作为接收者的通信。
• 微信视频聊天的两人能够同时看到对方的画面，双方既要同时发出视频信号，也要同时接收视频信号，这是一种双方同时都是接收者和发送者的通信。

单工(Simplex)：one-way的通信系统，一方为发送者，一方为接收者
半双工(Half Duplex)：two-way的通信系统，双方都是发送者，接收者，但是通信不能同时进行。
全双工(Full Duplex)：two-way的通信系统，双方同时发送与接收。

我们一般用Tx表示发送端，Rx表示接收端

例5：如果我有五根电线，那么我一次就能往线的另一头传输5bit的二进制数字，如果我只有一根线，那么我这5个bit的数字得一位一位传过去。

并行传输：一次性，同时传输n个bit
串行传输：将二进制数字一个一个传输。

3 信息量

我们之前提到过，信息蕴含在消息中，而对于接收者来说，真正要关心的是消息当中的不确定性。不确定性决定了信息量。

例6：这其实与编码是有关的。假设我们现在有一个八面体，要表示的消息是八面体抛掷后朝上的一面的结果。那么一共有八种可能性。我们现在用二进制码传输这个结果，二进制码来表示八种可能性，则需要三位，我们要传输3bit的二进制数。如果是十六面体呢？那需要4bit的二进制数。如你所见，随着面数增加，不确定性增加，需要编码的长度也变得越来越长，要传输的消息量(二进制位数)就越来越多。

这其实也反映了通信编码中的一个Philosophy：我们始终要用足够的长度来编码所有的可能性。

3.1 信息量计算

Shannon提出，信息量应该由以下公式计算

$$I(x) = \log_a \frac{1}{P(x)} = -\log_aP(x)$$

其中$x$是概率事件，$P(x)$表示x发生的概率。

• $a=2$，计算结果的单位是bit
• $a=e$，计算结果的单位是nit
• $a=10$，计算结果的单位是Hartley

对比于例6，每种可能性的概率是$1/8$，用二进制编码所需的位数是3，那么其实是有

$$2^3 = \frac{1}{1/8}$$

两侧同时取2为底的对数

$$3 = \log_2\frac{1}{1/8}$$

你会发现与我们的Shannon信息量计算公式是一样的形式！当$a=2$时，我们实际上是在使用二进制编码，信息量就是编码的长度，所以算出来的是bit。

3.2 Symbols and bits

例7：Alice的心情有开心和不开心两种状态，现在我们用0代表开心，1代表不开心，那么这是一个二进制的信息源，0或1的信息量都是1bit(假设Alice开心与不开心概率相等)。Bob的手游抽卡系统抽出的角色有四种稀有度：常见，一般，稀有，超稀有，我们用0代表常见，1代表一般，2代表稀有，3代表超稀有，那么这是一个四进制的信息源，0，1，2，3的信息量都是$2bit$(假设四种稀有度出现概率相等)

Symbols：是信息源的一种代表物，它是一种符号的集合，它代表着事件的每一种可能性。就如例7中两种心情状态，四种角色的稀有度。例6种八面体朝上那一面的可能性。
bits：是Symbols被编码之后的信息量

不难发现，对于一个M元Symbol的信息源，每个Symbol要包含$\log_2 M\ bit$的信息。

3.3 Entropy(熵)

Entropy代表着信息源提供的平均信息量，对于一个离散的信息源，我们有m个消息，每个消息的概率是$P(x_i)$，则Entropy计算为

$$H(x) = \sum_{i=1}^m p(x_i)\log_2 \frac{1}{p(x_i)}$$

Entorpy的单位是$bit/symbol$，即平均每个Symbol的信息量。

当信号是连续的时候，我们只需要简单地将求和换为积分

$$H(x) = -\int_{-\infty}^\infty p(x)log_2 p(x)dx$$

3.4 一些例子

（1）BSS全称Binary Symmetric Source，指的是输出是两个不同的symbol，其中一个symbol出现的可能性是$p$，另一个是$1-p$。根据熵的计算公式，我们很容易得到它的熵是

$$H(x) = -p\log_2 p-(1-p)\log_2(1-p)$$

最大熵：一条重要的性质是，当两个symbol出现的概率相等时，熵是最大的。在BSS中，就是$p=1-p=0.5$。让我们推广到k个symbols的信号源，当k个symbol出现概率相等时，有$p=\frac{1}{k}$，最大的熵为

$$H(x) = \sum_{i=1}^k p\log_2 \frac{1}{p}=k\times \frac{1}{k}\times \log_2\frac{1}{1/k}=\log_2k$$

Source Redundancy：我们定义Source Redundancy为

$$1-\frac{H(x)}{H_{max}(x)} = 1-\frac{H(x)}{\log_2 k}$$

从定义是不难看出，当源头的熵为最大熵(即等概)时，冗余为0，当熵小于最大熵时，我们就得到信息源的冗余程度。

（2）假设信息源是英文字母，那么当信息源等概时，我么能得到这个27symbols的信息源的最大熵为

$$H_{max}(x) = \log_2 27 \approx 4.75$$

但如果我们统计全世界已有英文文本中字母的出现频率，再根据熵公式计算，实际上的熵大概是$H=4.18$，那么Redundancy就是

$$1- \frac{4.18}{4.75}\approx 13\%$$

4 度量通信系统的性能

在前文提到过，我们希望通信系统有好的efficiency同时有好的Reliability，我们现在正式给出其定义
（1）efficiency：高效的传输消息，在合适的方法下传输最大量的消息。
（2）reliability：系统可靠地传输消息，一般依赖于系统的抗噪性能。

工程中，efficiency和reliability是一个tade-off，增加其中一个会导致另一个下降。

4.1 度量efficiency

（1）Efficiency的第一个度量就是传输的速度。在速度的度量中，我们有两个指标，Transmission symbol rate(传码率)和Transmission bit rate(传信率)。这是因为我们的信息源总是以symbol来定义的，就例如例7中Bob的游戏稀有度一样，有四个可能性，就意味着信息源是四元的。当我们想告诉别人Bob抽出了哪个稀有度的角色，我们只需要告诉他这四种可能性中的一个就行了。但当我们以二进制表示这四个Symbol的时候，每个Symbol需要两个bit编码，这个时候我们传输一个Symbol就意味着我们传输了两个bit。

Transmission symbol rate(传码率)：$R_B$，每秒传输的symbol数量，单位为是$Baud$。

Transmission bit rate(传信率)：$R_b$，每秒传输的bit数量，单位是$bit/s$，有时也写作$bps$，是bit per second的缩写。

现在我们给出$R_B$的计算方法，它的公式是

$$R_B=\frac{1}{T_s}$$

其中$T_s$是单个symbol在传输中的持续时间，称作transmission interval。

有些时候Symbol rate也写作$R_S$，单位可能把Baud缩写为B

那么怎么转换symbol rate和bit rate呢？从(3.2)中我们知道一个M元symbol包含$\log_2 M$个bit，那其实转换公式就显然了

Symbol rate转bit rate公式

$$R_b = R_B \log_2 M$$

其中$M$是信息源是几元的。

（2）efficiency另一个指标是频谱效率，它指的是在一个单位带宽中，我们最大能传输多少个bit，单位为$bit/s/Hz$。我们也可以广义的定义$\eta$

$$\eta_b = \frac{R_b}{B}(bit/s/Hz)\quad \eta=\frac{R_B}{B}(Baud/Hz)$$

这个公式告诉我们通信系统能多有效地利用有限的频谱资源，系统频谱效率越高，我们就能在更少的带宽内传输更多的bit。

4.2 度量reliability

在度量reliability时，我们主要是通过错误率来进行的。由于可以通过symbol度量，也可以通过bit度量，我们仍然有两种错误率
Baud Error Ratio：

$$P_e=\frac{收到的错误的symbol个数}{总共传输的symbol个数}$$

Baud Error Ratio：

$$P_b=\frac{收到的错误的bit个数}{总共传输的bit个数}$$

那通常情况下$P_e$和$P_b$谁大谁小呢？试想一个八进制信息源，我们需要三位二进制数字对其编码，将其传输三次，当错误一个symbol的时候，

$$P_e=\frac{1}{3}$$

当错误一个bit的时候

$$P_b=\frac{1}{9}$$

所以当使用M-ary信息源，$P_b<P_e$，但显然当信息源是二进制时，$P_b=P_e$

5 噪声

噪声是我们不想要的信号，它们在通信系统中混进我们想要传输的信号。例如在一场音乐会中，观众咳嗽的声音相较于音乐的声音就是噪声。

一个信号在传输过程中可能受到哪些噪声干扰呢？首先，宇宙环境中有各种辐射，人类各种电子设备也会散发辐射，这些都会影响电磁波传播，以上的称作External noise。

其次，传输设备内部也有噪声干扰，例如手机中或者交换机中电路对信号的干扰，尤其是热噪声。这种噪声称作Internal noise。

除了以上两种分类噪声的方式，根据噪声作用于系统的方式不同，还分为Additive noise和Multiplicative noise。加性噪声是相加到信号中去的$s'=s+n$，其中n是noise(噪声)。乘性噪声是与信号相乘的$s'=s\times n$。不难发现当$s=0$时，乘性噪声就消失了，但加性噪声仍然存在。

另外根据噪声本身的特性，也可以分为冲激噪声，它的波形一般是一个短暂的尖峰，例如突然发生的雷电。还有窄带噪声。有关窄带的内容将在后面介绍。

通信的传输无法避免噪声的干扰。

在这里我们引出信噪比的概念，信噪比就是信号与噪声的功率比较

$$SNR_{dB}=10\log_{10}\frac{S}{N}$$

其中S是信号功率，N是噪声功率。

不难发现，信噪比越大，意味着有用信号在接收信号中占比就越大。大信噪比好比在音乐会中音乐的声音远大过咳嗽的声音。如果音乐的声音很小，那就会显得咳嗽的声音很大，我们收听的质量就很差。

6 传输过程

6.1 对于传输资源的描述

（1）信道带宽：告诉我们目前信道最大能利用的带宽有多大，它定义为最大能传输的频率减去最小能传输的频率。$f_{max}-f_{min}$
（2）传输功率：指的是发出信号的时候功率有多大，这通常决定着信噪比，因为发出信号之后，信号就会在信道中受到各种噪声的影响，只要发出功率大，信噪比就越高。

6.2 传输损耗

由于材料会吸收电磁波等等原因，信号的功率或者振幅随着传输距离会降低，这称作Attenuation(衰减)。

噪声对信号可能造成波形的变化，让我们辨认不出原来的波形，这称作Distortion。

两根电线或者两个通讯设备靠的很近的时候，可能一个设备会干扰另一个设备，这叫做Interference。能够忽略两个设备相互干扰的最小距离称作Interference range

6.3 波形问题

假设我们要传输一段二进制码，二进制码在现实生活中可以用矩形波来表示，矩形波振幅为1的时候表示1，振幅为0的时候表示为0。

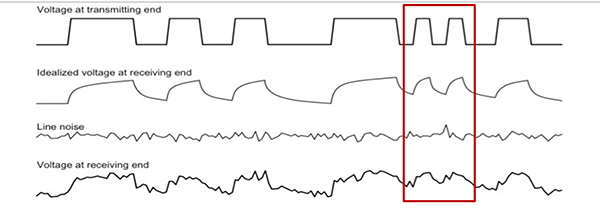
在传输的信号叠加噪声之后，波形可能失真程度很大。如果两个波峰挨得很近，那么极有可能在叠加噪声之后重叠在一起，一旦波峰重叠，我们将失去信号的特征，这是传输错误就发生了。于是，为了防止波峰重叠，我们需要考虑矩形波中波峰的距离。但是，这将直接影响我们传输的速度！如果矩形波能够由持续时间短且密集的波峰组成，那么在一小段时间里我们就能传输很多二进制码！

7 信道容量

既然信号的传输会因为噪声的影响而发生错误，那么给定一个信道，它最大能用多少的速度来传输bit而不出错呢？回顾之前看到的信道资源和影响信道的因素，它肯定和信道带宽和信噪比有关。

Shannon也给出了计算最大传输率的公式

$$C = B\log_2\left(1+\frac{S}{N}\right)$$

其中S是平均信号功率，N是平均噪声功率。这个公式计算出来的结果称作信道容量，它的意义是给定信道，信道理论上最大能够以多少速度传输bit而不出错。单位是$bit/s$.

Shannon公式计算出的最大传输速度实际上是指理论上，存在一个方法能在这个速度之下传输而不出错。它具有很强的工程指导意义。当我们想要达到某个传输速度的时候，我们可以选择合适的带宽和信噪比来设计我们的通信系统。

那么，我们是否可以无限增加带宽来提升信道容量呢？

答案是不行的。不幸的是，信道噪声的功率通常与带宽相关，我们在之后的学习中会常见的这个公式

$$N=n_0B$$

它意味着噪声功率和带宽成正比，正比的系数是$n_0$，这种噪声在之后的章节会学习到。

现在，我们使用这个公式更新我们的Shannon公式

$$C=B\log_2\left(1+\frac{S}{n_0B}\right)$$

注意到，当我们增加带宽的时候，信噪比不断缩小，那么式子中$\log_2(1+\frac{S}{N})$也在不断缩小，而B作为乘法因子在不断扩大，这显然是一个存在的极限！

$$\lim\limits_{B\rightarrow \infty}B\log_2\left(1+\frac{S}{n_0B}\right)\approx 1.44\frac{S}{n_0}$$

也就是说，就算我们无限制增大带宽，信道的容量也会有一个饱和的数值。我们无法获得无限的信道容量。