本文最后更新于:2024年3月12日 晚上
1 Introduction
Mamba是一次用状态空间模型来做深度学习的Foundation Model的尝试,原论文是《Mamba: Linear-Time Sequence Modeling with Selective State Spaces》,arXiv: 2312.00752.
2 前置知识:状态空间模型
2.1 连续情况
状态空间模型在控制系统中常见,其目的是建立一个输入到中间状态(latent state)再到输出的关系。假设输入的信号是u(t),中间状态是x(t),输出为y(t),那么状态空间模型可由两个方程表示
{x′(t)=Ax(t)+Bu(t)y(t)=Cx(t)+Du(t)
方程1是一个关于中间变量和输入信号的微分方程,可以解出x(t),可以看作对状态之间和输入的建模,方程2则建立了输出,状态和输入的关系。
论文中忽略参了参数D,或者说D=0,作者在S4模型中解释为因为项Du(t)可看作模型的“跳跃连接”。如果我们只看方程2,那么抛开状态x(t)所做的变换,y(t)=[ ⋅ ]+Du(t)实际上建立了一条从输入u(t)直接到输出y(t)的路径,只不过乘上了参数D。
2.2 离散化
计算机系统无法处理连续的微分方程,而离散化状态空间模型已经是一个well-studied问题,本文中采用ZOH方法来进行离散化,具体来说,如果我们记
{A=exp(ΔA)B=(ΔA)−1(exp(ΔA−I)⋅ΔB)
其中Δ为一个可调参数,我们称作步距(step size),这个参数实际上也作为可学习参数让模型自己学。那么我们可以将状态空间模型写成序列递推的形式
{hk=Ahk−1+Bukyk=Chk
方程1中已经不需要计算微分方程,而改为计算一个关于hk−1到hk的递推方程。我们可以把hk∈RN看作一个RNN里面的隐藏状态(hidden state),而矩阵A是过渡矩阵(transition matrix)。
2.3 卷积并行化
到这里,状态空间模型仍然是递推的,也就意味着无法并行化,但注意其与RNN不同的地方,状态之间的过渡是没有激活函数的,这意味着我们可以迭代这个公式来提前计算中间结果。具体来说,假设初始状态h−1=0,那么迭代方程hk=Ahk−1+Buk可以显式的得到
h0=Bu0y0=CBu0h1=ABu0+Bu1y1=CABu0+CBu1h2=A2Bu0+ABu1+Bu2y2=CA2Bu0+CABu1+CBu2…
对于第k个时间点,可以显式地将yk写出来
yk=CAkBu0+CAk−1Bu1+⋯+CABuk−1+CBuk
我们把它写成两个向量点乘
yk=CAkBu0+CAk−1Bu1+⋯+CABuk−1+CBuk=⎣⎢⎢⎢⎢⎢⎡CAkBCAk−1B⋯CABCB⎦⎥⎥⎥⎥⎥⎤⋅⎣⎢⎢⎢⎢⎢⎡u0u1⋯uk−1uk⎦⎥⎥⎥⎥⎥⎤
我们对于一个确定的序列长度k+1,可以记
K=⎣⎢⎢⎢⎢⎢⎡CAkBCAk−1B⋯CABCB⎦⎥⎥⎥⎥⎥⎤
那么序列y=[y0,y1,…,yk]实际上可以由卷积
y=K∗u
计算,具体来说,我们举一个长度为3的序列的例子,
u=⎣⎢⎡u0u1u2⎦⎥⎤K=⎣⎢⎡CA2BCABCB⎦⎥⎤y=⎣⎢⎡y0y1y2⎦⎥⎤
我们对输入序列前pad个数等于dimu−1的0元素,得到
u=⎣⎢⎢⎢⎢⎢⎡00u0u1u2⎦⎥⎥⎥⎥⎥⎤
然后,我们将K当作滑动窗口与u对齐并滑动,
⎣⎢⎡CA2BCABCB⎦⎥⎤⎣⎢⎢⎢⎢⎢⎡00u0u1u2⎦⎥⎥⎥⎥⎥⎤
卷积核从第一个元素位置开始向下滑动并做点积,结果为
y0y1y2=CA2B⋅0+CAB⋅0+CB⋅u0=CBu0=CA2B⋅0+CAB⋅u0+CB⋅u1=CABu0+CBu1=CA2B⋅u0+CAB⋅u1+CB⋅u2=CA2Bu0+CABu1+CBu2
与我们之前递归计算的结果是一样的。也就意味着,这个模型可以以卷积的形式,提前算出卷积核并与输入做卷积运算,这就实现了并行化计算。
2.4 HiPPO矩阵
另一个值得注意的技术是作者对矩阵A用了特殊的初始化技巧,具体来说,A会被初始化为下面这个矩阵
Ank=⎩⎪⎪⎨⎪⎪⎧(2n+1)1/2(2k+1)1/2n>kn+1n=k0n<k
这是因为之前随机初始化矩阵A的时候效果并不好,所以使用HiPPO矩阵进行初始化,它能够很好的压缩历史记忆,对于近期的信息衰减较小,而对于过往的记忆衰减较大。如果我们以一个4×4的方阵为例,HiPPO矩阵为
⎣⎢⎢⎢⎡1111023300350004⎦⎥⎥⎥⎤
3 Mamba模型
3.1 动机
作者认为,序列建模的一个基本问题在于怎么把上下文压缩到一个更小的状态,例如Attention就完全不压缩上下文,我们在自回归计算的时候显式地存储了整个上下文(KV-Cache)。所以Transformer是effective and inefficient。而循环的模型(RNN和状态空间模型)都有一个有限的状态,而压缩上下文到这个状态的好坏就决定了这类模型的effectiveness。
在这里作者举了两个例子,一个是复制任务,一个是选择性复制任务。
复制任务定义为,给定一个序列,模型学习将序列的元素复制到几个时间点后的地方,例如原序列为[1,2,3,4,0,0,0,0],模型学习将其复制到[0,0,0,0,1,2,3,4]。
选择性复制则稍有不同,它要求模型将序列选择性的复制到几个时间点后,例如给定序列[1,2,x,3,0,0,0,0],模型要学会忽略x,将数据复制为[0,0,0,0,0,1,2,3]。原序列中x的位置和个数都是随机的。
Induction Heads任务要求模型通过序列“回忆”输入序列,根据上下文来检索答案,例如给定序列[1,x,3,4,0,0,1,?],其中?要求模型填入下一项,那么模型将需要检索上下文,发现1后面会跟上x,然后推断出下一项为x。这是LLM的一项关键能力。
作者认为,时不变模型,也就是之前的S4模型,参数是固定的,不随输入变化的,这导致模型无法进行内容感知(content-aware)推理。在选择性复制任务中,模型无法根据输入内容中要忽略token的位置和个数来选择性忽略(Optimization只能让模型学会忽略一个固定的pattern),Induction Heads任务也是如此,我们无法以不依赖输入的方式影响沿着序列传递的隐藏状态。
所以作者决定,将S4模型中的参数改成input-dependent。
3.2 S6算法
之前S4模型的算法是
Input: x: (B, L, D)
Output: y: (B, L, D)
- A: (D, N) <- Parameter # 初始化矩阵A
- B: (D, N) <- Parameter # 初始化矩阵B
- C: (D, N) <- Parameter # 初始化矩阵C
- Δ: D <- τΔ(Parameter) 初始化Δ
- A,B: (D, N) <- discretize(Δ,A,B) # 离散化矩阵
- y <- SSM(A,B,C)(x) # SSM计算
- return y
在这里τΔ是一个激活函数,为softplus,具体来说,
softplus(x)=log[1+exp(x)]
可看作平滑的ReLU。
更改后的算法(叫做S6)为
Input: x: (B, L, D)
Output: y: (B, L, D)
- A: (D, N) <- Parameter # 初始化矩阵A
- B: (B, L, N) <- sB(x) # 映射输入为矩阵B
- C: (B, L, N) <- sC(x) # 映射输入为矩阵C
- Δ: (B, L, D) <- τΔ(Parameter+sΔ(x)) # 映射与随机参数共同决定Δ
- A,B: (B, L, D, N) <- discretize(Δ,A,B) # 离散化矩阵
- y <- SSM(A,B,C)(x) # SSM计算
- return y
其中
⎩⎪⎪⎨⎪⎪⎧sB(x)=LinearD→N(x)sC(x)=LinearD→N(x)sΔ(x)=BroadcastD[LinearD→1(x)]
所以,S6算法实际上只是多使用了一层映射将参数矩阵与输入联系起来,从而达到参数随着输入动态变化的效果。
笔者注:这里shape可能对不上,代码中计算矩阵乘法是这样的:
deltaA = torch.exp(torch.einsum('bdl,dn->bdln', delta, A))
,而代码中Δ的shape就是(B, D, L)。与输入做乘法的时候也是这样:
deltaB_u = torch.einsum('bdl,bnl,bdl->bdln', delta, B, u)
迭代计算的部分是
x = deltaA[:, :, i] * x + deltaB_u[:, :, i]
注意在这里,u为输入,x为中间状态。x初始化为
x = A.new_zeros((batch, dim, dstate)) shape: (B, D, N)
但现在就出现了一个问题,即然参数随着输入变化了,那模型就是一个time-varying的系统,之前提前算卷积核然后用卷积方式并行计算的trick就不能用了。为了避免完全迭代计算,作者使用了三个trick来进行加速,分别是Kernel Fusion,Parallel Scan和Recomputation。
3.3 高效地实现S6算法
3.3.1 Kernel Fusion
现代GPU加速器一般有两个内存空间,HBM(High-Bandwidth Memory)和SRAM(Static Random-Access Memory)。这构成了GPU的内存层级。我们知道,内存分层级则意味着速度快的内存小,内存大的速度慢。HBM则是慢的那个,SRAM是快的那个。
GPU运算的时候,会将数据从HBM加载到SRAM中,运算完毕后再存回HBM。那么如果我们用多个CUDA Kernel来处理Mamba的迭代过程,就会导致多个Kernel对两个内存的读写。
例如,我们以三个CUDA Kernel为例,那么kernel1读取HBM的数据到SRAM,处理之后返回到HBM,Kernel2读取HBM中的结果开始处理,结果又存回HBM,Kernel3再读取HBM里的结果处理后再存回HBM。这些kernel可能 是负责离散化,迭代和最后输出的与矩阵C的矩阵乘法的。作者则把离散化,迭代(后续替代为Parallel scan)和矩阵乘法写到一个自定义的Kernel里面,这样就把几个不同的Kernel融合为一个,叫做Kernel Fusion。
具体来说,他们在一个CUDA Kernel内做以下步骤
- 从HBM中读取Δ, A, B, C到SRAM中
- 在SRAM中离散化,得到A,B
- 做parallel scan,在SRAM中得到中间状态
- 乘矩阵C,得到最终结果并写回HBM
作者声称能提速20-40倍。
3.3.2 Parallel Scan
Parallel scan是使用并行化的方法来进行序列操作,最开始是用在prefix-sum问题上。给出一个序列[1,2,3,4,5], prefix-sum指对前n个元素进行求和,n∈[1,k], k为序列长,得到序列[1,3,6,10,15]。这个问题用for-loop当然可以很简单的解决,但它可以用多线程来并行计算。
给定一个长度为8的输入序列[x1,x2,x3,x4,x5,x6,x7,x8],我们按以下方式计算,首先开四个线程分别计算得到
a=[x1+x2],b=[x3+x4],c=[x5+x6],d=[x7+x8]
再开两个线程计算上面得到的结果,得到
e=[x1+x2+x3+x4],f=[x5+x6+x7+x8]
最后一个线程求和得到
g=[x1+x2+x3+x4+x5+x6+x7+x8]
上述过程叫Up-Sweep。我们利用以上得到的结果和原序列,按照以下方式再次计算。首先一个线程计算得到
h=e+c=[x1+x2+x3+x4+x5+x6]
再开四个线程计算得到
a+x3=[x1+x2+x3],e+x5=[x1+x2+x3+x4+x5]h+x7=[x1+x2+x3+x4+x5+x6+x7]
上述过程称为Down-Sweep, 此时我们已经得到了完整的prefix-sum,为
[x1,a,a+x3,e,e+x5,h,h+x7,g]
Mamba的迭代过程可以定义为类似于prefix-sum的问题,假设prefix-sum的输入是x=[xi],其输出是为y=[yi],那么关系为yi=yi−1+xi。上述Mamba的状态迭代方程为hk=Ahk−1+Buk,抛开多乘了两个参数,这两个关系式的形式是Identical的。所以我们可以使用Parallel Scan来并行化Mamba的计算。
3.3.3 Recomputation
作者提到,他们为了节省显存,他们carefully使用Recomputation技巧,也就是前向过程不存储中间状态,而是在反向传播的时候再重新计算,具体的操作在论文附录中有提到,这一部分应该不难阅读。
3.4 Mamba Block
这一部分就是喜闻乐见的搭积木环节了,block如下
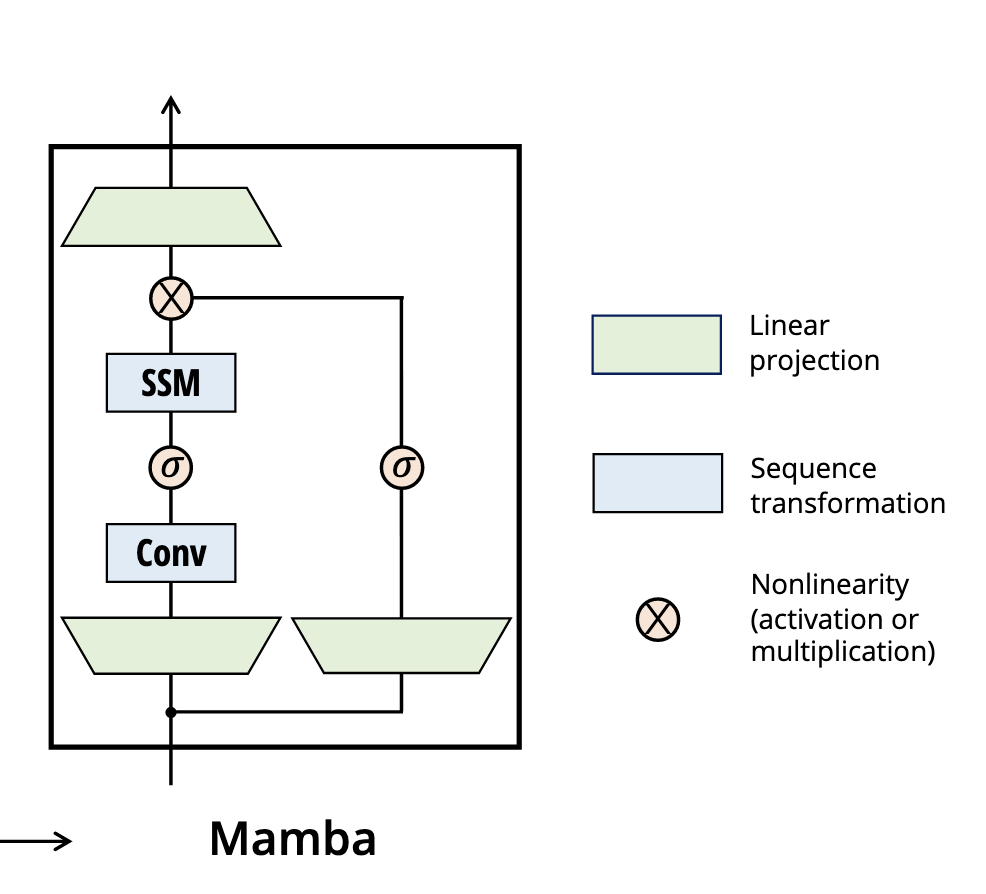
注意这里作者并没画全所有的Module,完整的block大概是这个样子
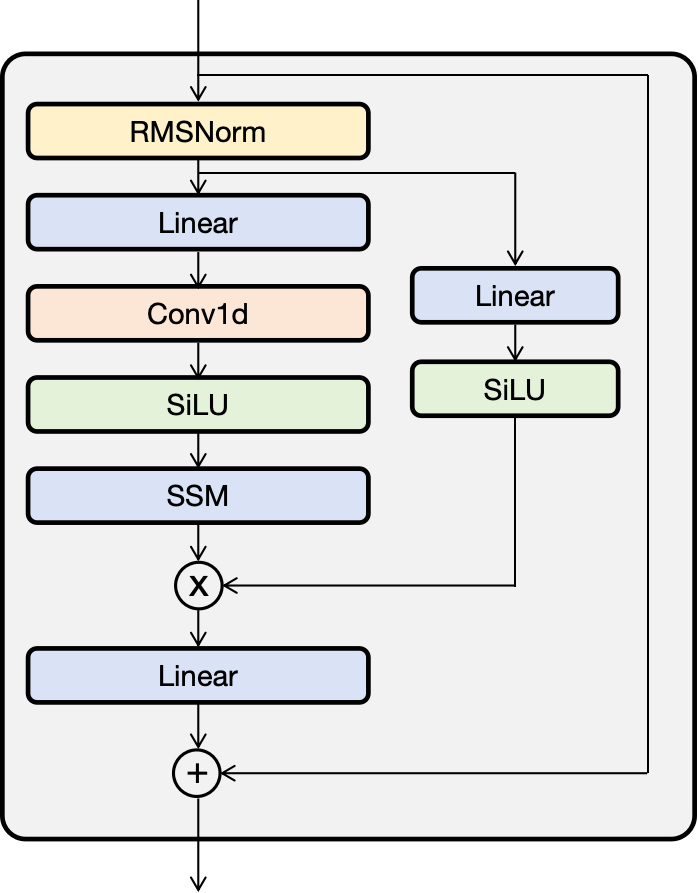
4 总结
已经有好几个声称能媲美或打败Transformer的模型了,他们应该有种种缺点所以最终没有被大规模采用。Mamba可以说是少见的被follow的很快的工作,但个人感觉在某些方面应该还是比不过Transformer。最近谷歌在3月1日新发了Griffin和Hawk模型(arXiv:2402.19427),好像还没开源,可以观望一下。
也佩服作者Albert Gu的毅力,S4模型,HiPPO矩阵等工作都有他的参与,可谓是一路下来把状态空间模型从不work改进到work。Griffin论文中也见到了Albert Gu的参与。

